技術資料 一般編 9
配管内を流れる液体の流量と圧力の関係 注意事項 ![]()
| 流量と圧力の関係 (液体の場合) 配管内を流れる流体の流量と流速の関係は Q=C×A×V で表せます。 ここで、Q:流量 C:流量係数 A:流路面積 V:流速 V=(2×P÷ρ)^0.5 ベルヌーイの定理の応用より Pv = 1/2 × ρ × V ^2 Pv :動圧 Q=C×A×(2×P÷ρ)^0.5 Q:流量 m^3/sec P:圧力 差圧(パスカル) ρ(ロー):流体密度 kg/m^3 P=(Q÷(C×A))^2×(ρ÷2) 液体の場合を考えてみると 内径150mmの水平配管に、100m3/h の流量で水が流れていて、その時の配管内の圧力が 100kPa(G) とし、配管下流にバルブが設置されていてバルブの2次側が大気開放されているとします。 配管内の圧力が 200kPa(G) に上昇した場合の流量はいくらになるか? 配管の下流側の負荷(抵抗)は変わらず、配管2次側のバルブを操作しないとして考え Q=C×A×(2×P÷ρ)^0.5 式の Q=100m3/h P=100kPa(G) ρ=1000kg/m3 を代入することで求められます。ここで C 、 A 、 2 の項は一定と考え、式から省きます。 流量Qは(P÷ρ)^0.5 に比例します、つまり圧力Pの平方根に比例し、密度ρの平方根 に反比例します。 配管下流側の負荷(抵抗)は変わらないとすると、圧力Pは配管内の圧力の変化として考えること ができるので、上昇した圧力 200kPa(G) と元の圧力 100kPa(G) の比として考えることができます。 つまり、200÷100 = 2 圧力Pが2倍になったことになります。 流量Qは圧力Pの平方根に比例するので、√2 = 1.4142 になり、流量は 1.4142 倍になります。 水の密度ρは圧力が変わっても変わらないのでρ(ロー)の項は計算は不要となります。 圧力が200kPa(G)に上昇した時は Q=C×A×(2×2÷ρ)^0.5 となり 流量は 100m3/h × 1.4142 = 141.42 m3/h になります。 このときの流速 V は、V=(2×P÷ρ)^0.5 ベルヌーイの定理の応用より、圧力が2倍になるので 流速 V は √2 = 1.4142 、流速は 1.4142倍になります。 ベルヌーイの定理とはエネルギー保存の法則を流体に当てはめたものですが、上のベルヌーイ の定理の応用とは圧力と流速および流体密度の関係式であって、圧力が上がる(ポンプ圧など) と流速が速くなり流量が大きくなる関係式を求めるものであり、圧力のエネルギーが変化した場合です。 この圧力(動圧):Pと流速:V、流体密度:ρの関係式はベルヌーイの定理より求めています。 (水平配管内を流れる水の圧力変化による流量変化を考え、位置エネルギー及び粘性の影響 は無いものとして考えた場合です。) 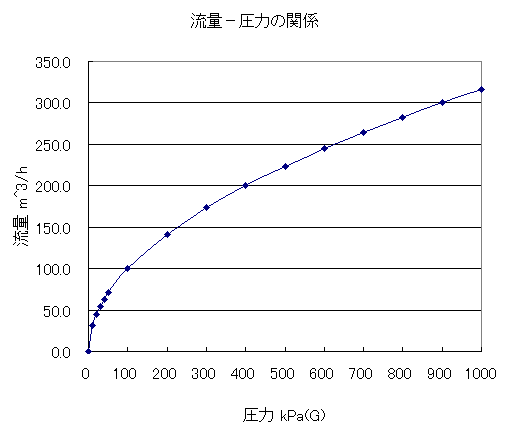 配管内を流れる水の圧力と流量の関係は上のグラフになります。 流量は圧力の平方根に比例し、圧力は流量の2乗に比例します。 流量を2倍に増やすには圧力を4倍にする必要があります。 流量を1/2(半分)にするには圧力を1/4にします。 |
圧力配管内を流れる水の流量の計算 基本式 Q=C×A×(2×P÷ρ)^0.5 |
上に掲載した資料は弊社流量計の性能に影響する内容ではありませんので 全ての項目について問い合わせには応じられません。 |